This CMI-funded research was conducted at Ames Laboratory in a collaboration between CMI projects Finite Element Modeling of Magnetic and Electrochemical Systems (2.1.13) and Reduced Rare Earth Content High Performance Magnets (2.1.14).
Achievement:
- Assessed potential for using Ce-Co-Cu magnets in high speed motors applications
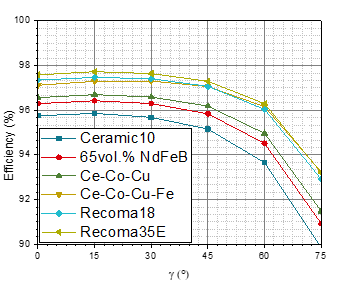
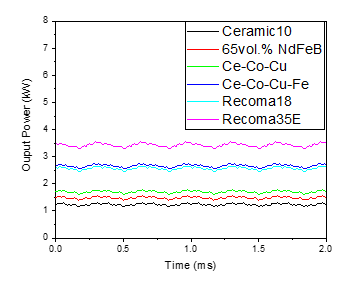
- Ce-Co-Cu outperformed bonded magnets and ceramic (ferrite) magnets while performing acceptably compared with Sm-Co
- Identified areas for future improvement
Significance and Impact:
- Ce-Co-Cu is being investigated as a potential gap magnet. Our results demonstrate how Ce-Co-Cu fits in the gap, compared with other commercial magnets
- Provides opportunity to engage with potential industrial partners. Ce-Co-Cu if deployed commercially as substitute for Sm-Co, may save processing cost and reduce the use of Co
Details and Next Steps:
- Improve model based on recent improvements to chemistry
- Sm-Co magnets are known for high temperature performance. Modeling will be extended to high temperature performance of Ce-Co-Cu magnets to compare losses in both materials