CMI scientists at Idaho National Laboratory conducted this research.
Achievement:
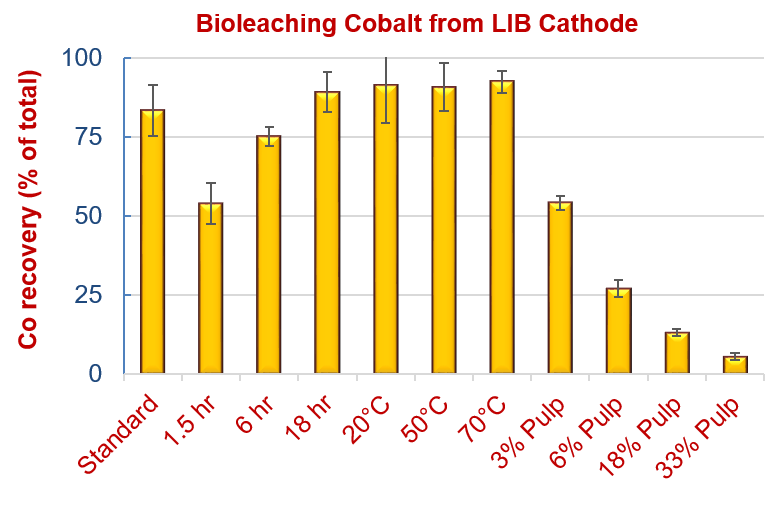
Processing parameters of bioleaching time, temperature and pulp density on Co recovery from lithium ion battery cathode powder were optimized. Optimal conditions were found for temperatures between 20-70°C and incubation times >18 hours. Increasing pulp density (solid mass : liquid mass) from 1.5% to 3% and 6% led to 35% and 65% reduction in leaching efficiency, respectively.
Significance and Impact:
The results provide guidance for starting conditions for future scale-up research
Approach:
- Apply optimized conditions to simulated heap-leaching process
- Test mixed lithium ion battery waste materials
