Weyl semimetal may be thought of as a gapless topological phase protected by the chiral anomaly, where the symmetries involved in the anomaly are the charge conservation and the crystal translational symmetry. One experimental manifestation of the chiral anomaly is a charge current in parallel electric and magnetic fields, with the magnetoresistance decreasing with increasing magnetic field. The absence of a band gap in a weakly-interacting Weyl semimetal is mandated by the electronic structure topology and is guaranteed as long as the symmetries and the anomaly are intact.
The nontrivial topology manifests itself in the topological response, in particular taking the form of an anomalous Hall effect in magnetic Weyl semimetals, whose magnitude is only determined by the location of the Weyl nodes in the Brillouin zone. We consider the situation when the interactions are not weak and ask whether it is possible to open a gap in a magnetic Weyl semimetal while preserving its nontrivial electronic structure topology along with the translational and the charge conservation symmetries. Surprisingly, the answer turns out to be yes. The resulting topologically ordered state provides a nontrivial realization of the fractional quantum Hall effect in three spatial dimensions in the absence of an external magnetic field. Furthermore, this state cannot be viewed as a stack of two-dimensional states.
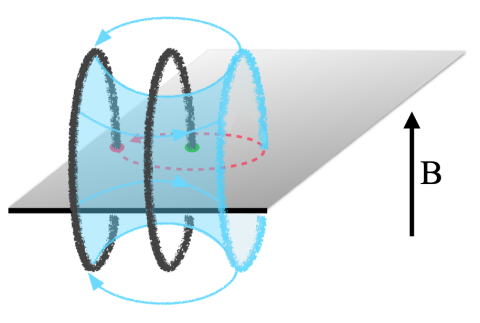
Our state contains loop excitations with nontrivial braiding statistics when linked with lattice dislocations. The braiding statistics of this exotic state may have applications in quantum computing.
Chong Wang, L. Gioia, and A.A. Burkov, Fractional Quantum Hall effect in Weyl semimetals, Phys. Rev. Lett. 124, 096603 (2020).
